Числа с плавающей запятой
Представление чисел в виде ЧПЗ позволяет избавиться от операции масштабирования при вычислениях, поскольку диапазон представляемых чисел существенно расширяется по сравнению с ЧФЗ. Однако в большинстве ЭВМ общего назначения, для целых чисел сохраняется возможность представления в виде ЧФЗ. Операции с ЧФЗ всегда выполняются за меньшее время, чем операции с ЧПЗ. В частности, к операциям с целыми числами сводятся операции над кодами адресов (операции индексной арифметики).
Представление чисел с плавающей запятой в общем случае имеет вид:
X = Sp*q; |q|<1,
где q – мантисса (правильная дробь со знаком),
p – порядок (целое число со знаком),
S – основание,
Sp – характеристика.
В ЭВМ q и p представлены в системе счисления с основанием S в соответствующей двоичной кодировке. Знак числа совпадает со знаком мантиссы. Порядок может быть как положительным, так и отрицательным и определяет положение точки в числе X. Арифметические действия над ЧПЗ требуют помимо действий с мантиссами, определенные операции над порядками (сравнение, вычитание и др.). Для упрощения операций над p их сводят к действиям над целыми положительными числами, применяя представление ЧПЗ со смещенным порядком.
В этом случае к порядку p прибавляют целое число R=2k, где k – число двоичных разрядов, используемых для представления модуля порядка. Смещенный порядок PСМ=P+R всегда больше нуля или равен ему. Для его представления требуется такое же количество двоичных разрядов, как и для представления знака и модуля p.
При фиксированном числе разрядов мантиссы любая величина представляется в ЭВМ нормализованным числом с наибольшей возможной точностью. Число называется нормализованным, если мантисса q удовлетворяет условию 1>|q|³1/S, т.е. старший разряд мантиссы в S-ричной системе счисления отличен от нуля, иначе число не нормализовано. Так, например, в десятичной системе счисления число 0.00726*10-3 не нормализовано, а число 0.726*10-5 – нормализовано.
В процессе вычислений числа могут оказаться ненормализованными. Обычно ЭВМ автоматически нормализует такие числа, выполняя ряд действий. На рис. 2.9 представлен обобщенный формат представления ЧПЗ в микро- и миниЭВМ.
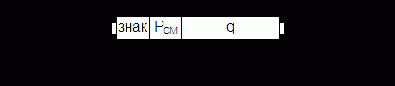
Пусть r старших разрядов S-ричной мантиссы равны нулю. Тогда нормализация состоит:
- из сдвиг мантиссы на r разрядов влево;
- уменьшения PСМ
на r единиц;
- запись нуля в r младших разрядах мантиссы.
При этом число не изменяется, а условия нормализации выполняются.
Пример.
Нормализовать двоичное число.
Ненормализованное двоичное число:

Нормализованное двоичное число:

Пример.
Нормализовать двоичное число.
Ненормализованное двоичное число:

Нормализованное двоичное число:

Следует иметь в виду, что нормализация может происходить в другую сторону, если в результате выполнения операции слева от точки появилась единица. В этом случае необходимо выполнить следующие операции:
- сдвиг мантиссы на один разряд вправо;
- увеличение PСМ
на единицу.
В различных ЭВМ числа с плавающей запятой используются в системах счисления с различными основаниями S, но равными целым степеням числа 2, т.е. S=2W. При этом порядок представляют целым числом, а мантиссу q – числом, в котором группы по W двоичных разрядов изображают цифры мантиссы с основанием системы счисления S=2W. В современных ЭВМ используются, как правило, S = 2, 16.
Использование S>2 позволяет:
- расширить диапазон представления чисел;
- ускорить выполнение операций нормализации, поскольку сдвиг может сразу происходить на несколько разрядов (при S=16 – сдвиг на 4 разряда).
Пример.
В результате операции получили (S=16):

Произведем нормализацию. Для этого q нужно сдвинуть влево на один шестнадцатеричный разряд, т.е. на 4 двоичные единицы, а из P вычесть 1. В результате получим

Итак, диапазон представляемых в ЭВМ чисел с плавающей запятой зависит от основания системы счисления S и числа разрядов, выделенных для P.
Точность вычисления для ЧПЗ определяется числом разрядов q. С увеличением числа разрядов q увеличивается точность, но одновременно увеличивается и время выполнения арифметических операций. Ввиду этого использование S, отличного от 2, несколько уменьшает точность вычислений при фиксированном числе двоичных разрядов q. Традиционно шестнадцатеричная арифметика используется в мэйнфреймах.
Задачи, решаемые на ЭВМ, предъявляют различные требования к точности вычисления, поэтому большинство машин общего назначения имеют несколько форматов ЧПЗ с различным числом разрядов q. Рассмотрим только короткие форматы ЧПЗ в ЭВМ с 32-разрядным словом, использующих шестнадцатеричную (S=16) и двоичную (S=2) системы счисления.
Формат ЧПЗ при S=16 представлен на рис. 2.10.

Всего под q отведено 24 двоичных разряда. Общая длина слова N – 32 двоичных разряда. Еще есть длинный формат (64 бита) и расширенный (128 бит). Во всех форматах под PСМ отведено по 7 двоичных разрядов (с первого по седьмой). Если бы порядок был несмещенный, то один двоичный разряд отводился бы под знак порядка и k разрядов – под модуль (k = 6). При этом диапазон изменения модуля несмещенного порядка P составил бы 0 ¸ 2k-1 или 0 ¸ 63, а полный диапазон изменения порядка Р = (-64) ¸ (+63). Выражение для смещенного порядка соответственно имеет вид

Таким образом, при S=16 диапазон изменения PСМ = 0 ¸ 127.
Следует иметь в виду, что при изображении машинного слова с помощью шестнадцатеричных символов первые две старшие шестнадцатеричные цифры представляют совместно знак числа и смещенный порядок.
Формат ЧПЗ при S=2 представлен на рис. 2.11.

Общая длина слова N – 32 двоичных разряда. Обычно еще есть длинный формат, имеющий N = 64 бита. В обоих форматах под смещенный порядок отведено 8 двоичных разрядов. Таким образом, диапазоны изменения смещенного и несмещенного порядков составляют соответственно
PСМ
= 0...255 и P = -128...+127 .
Поскольку числа в памяти хранятся в нормализованной форме, старший разряд q всегда равен единице, поэтому он не запоминается, а подразумевается., В таких ЭВМ точность представления числа фактически определяется мантиссой q в 24 двоичных разряда (короткий формат) и 56 двоичных разрядов (длинный формат).
Рассмотрим только короткие форматы.
Диапазон представления ЧПЗ определяется значением S и числом разрядов, отведенных под P.
Двоичное основание (S=2): (k=7) Xmax=2127® 1038 .
Шестнадцатеричное основание (S=16): (k=6) Xmax=1663® 1076 .
Точность представления ЧПЗ определяется значением S и числом разрядов мантиссы в соответствующей системе счисления. И при S=16, и при S=2 под q отведено фактически 24 двоичных разряда:
- при S=2: 24 двоичных разряда обеспечивают точность, соответствующую семи десятичным разрядам;
- при S=16: точность при использовании короткого слова (N = 32) ниже за счет другого способа нормализации, т.е. в q могут быть три нуля слева, поскольку шестнадцатеричное число при этом еще не равно нулю. В двоичных числах слева всегда единица, то есть разрядная сетка используется полнее. Пояснить это можно на примере 8-разрядной сетки:

При S=16 нормализация не произойдет, так как d1 не равно нулю. Это приведет к потере четырех младших разрядов результата. При S=2 нормализация произойдет и будет потерян только один младший разряд результата. В связи с этим в ЭВМ с S=16 обычно предусматриваются еще длинный и расширенный форматы.
Еще до недавнего времени каждый производитель процессоров пользовался собственным представлением вещественных чисел (чисел с плавающей точкой). За последние несколько лет ситуация изменилась. Большинство поставщиков процессоров в настоящее время для представления вещественных чисел придерживаются стандарта ANSI/IEEE 754-1985 Standard for Binary Floating-Point Arithmetic.
Стандарт описывает два основных формата ЧПЗ: одиночный (single – 32 бита) и двойной (double – 64 бита). В IEEE 754 не указан точный размер расширенного формата, но описаны минимальная точность и размер (79 бит).
Формат числа – структура, определяющая поля, составляющие число с плавающей запятой, их размер, расположение и интерпретацию.
Одиночный формат
Одиночный формат состоит из трех полей: 23-разрядной мантиссы f, 8-разрядного смещенного порядка e, знакового бита s (см.
рис. 2.12).

В табл. 2. 3 показано соответствие между значениями трех полей и значением числа с плавающей запятой.
Таблица 2.3
|
Комбинация значений полей |
Значение |
|
0 < e < 255 |
(-1)s × 2e-127 × 1.f (нормализованные числа) |
|
e= 0; f ¹ 0 (по крайней мере, один бит не нулевой) |
(-1)s × 2-126 × 0.f (ненормализованные числа) |
|
e= 0; f = 0 (все биты нулевые) |
(-1)s × 0.0 (ноль со знаком) |
|
e= 255; f = 0 (все биты нулевые) |
INF (бесконечность со знаком) |
|
e= 255; f ¹0 (по крайней мере, один бит не нулевой) |
NaN (Not-a-Number) |
Двойной формат
Двойной формат состоит из трех полей: 53-разрядной мантиссы f, 11-разрядного смещенного порядка e, знакового бита s. Эти поля хранятся в двух 32-разрядных словах, как показано на рис. 2.13. В x86–архитектуре слово с меньшим адресом содержит младшие разряды мантиссы, в то время как, например, в SPARC– архитектуре младшие разряды мантиссы содержит слово с большим адресом.

В табл. 2.4 показано соответствие между значением трех полей и значением ЧПЗ двойной точности.
Таблица 2.4
|
Комбинация значений полей |
Значение |
|
0 < e < 2047 |
(-1)s × 2e-1023 × 1.f (нормализованное число) |
|
e = 0; f ¹ 0 |
(-1)s × 2-1022 × 0.f (ненормализованное число) |
|
e = 0; f = 0 |
(-1)s × 0.0 (ноль со знаком) |
|
s = 0; e = 2047; f = 0 |
+INF (положительная бесконечность) |
|
s = 1; e = 2047; f = 0 |
-INF (отрицательная бесконечность) |
|
e = 2047; f ¹ 0 |
NaN (Not-a-Number) |
Расширенный формат (SPARC– архитектура)
Расширенный формат состоит из трех полей: 112-разрядной мантиссы f,
15-разрядного смещенного порядка e, знакового бита s. Эти поля хранятся в четырех 32-разрядных словах, как показано на рис. 2.14. В SPARC–архитектуре младшие разряды мантиссы содержит слово с большим адресом.

В табл. 2.5 показано соответствие между значением трех полей и значением ЧПЗ расширенного формата для SPARC–архитектуры.
Таблица 2.5
|
Комбинация значений полей |
Значение |
|
0 < e < 32767 |
(-1)s × 2e-16383 × 1.f (нормализованное число) |
|
e = 0; f ¹ 0 |
(-1)s × 2-16382 × 0.f (ненормализованное число) |
|
e = 0; f = 0 |
(-1)s × 0.0 (ноль со знаком) |
|
s = 0; e = 32767; f = 0 |
+INF (положительная бесконечность) |
|
s = 1; e = 32767; f = 0 |
-INF (отрицательная бесконечность) |
|
e = 32767; f ¹ 0 |
NaN (Not-a-Number) |
Расширенный формат состоит из 4-ч полей: 63-разрядной мантиссы f, явного старшего значащего бита j, 15-разрядного смещенного порядка e, знакового бита s.
В х86–архитектуре эти поля сохранены в восьми последовательно адресованных 8-разрядных байтах. Однако UNIX System V Application Binary Interface Intel 386 Processor Supplement (Intel ABI) требует, чтобы числа расширенного формата занимали три последовательно адресованных 32-разрядных слова в стеке, оставляя 16 старших бит неиспользованными, как показано на рис. 2.15.

В табл. 2.6 показано соответствие между значениями трех полей и значением ЧПЗ расширенного формата для х86–архитектуры.
Таблица 2.6
|
Комбинация значений полей |
Значение |
|
j = 0; 0 < e < 32767 |
Не поддерживается |
|
j = 1; 0 < e < 32767 |
(-1)s × 2e-16383 × 1.f (нормализованное число) |
|
j = 0; e = 0; f ¹ 0 |
(-1)s × 2-16382 × 0.f (ненормализованное число) |
|
j = 1; e = 0 |
(-1)s × 2-16382 × 0.f (псевдоненормализованное число) |
|
j = 0; e = 0; f = 0 |
(-1)s × 0.0 (ноль со знаком) |
|
j = 1; s = 0; e = 32767; f = 0 |
+INF (положительная бесконечность) |
|
j = 1; s = 1; e = 32767; f = 0 |
-INF (отрицательная бесконечность) |
|
j = 1; e = 32767; f ¹ 0 |
quiet или signaling NaN |
Мэйнфреймы
В мэйнфреймах фирмы IBM используемое еще со времен S/360 шестнадцатеричное представление чисел с плавающей запятой – с шестнадцатеричной мантиссой и характеристикой (HFР) – в ESA/390 (мэйнфреймы серии S/390) дополнено двоичным представлением BFP, удовлетворяющим стандарту IEEE 754. Это представление определяет 3 формата данных – короткий, длинный и расширенный– и 87 новых команд для работы с ними.
BFP появилось в ESA/390 относительно недавно, в 1998 году. Одновременно было введено 12 дополнительных регистров FR (общее число FR достигло 16). Кроме того, в архитектуре появился управляющий регистр с плавающей запятой и средства сохранения содержания регистров при операции записи состояния. Добавлено еще 8 новых команд, не связанных однозначно с тем или иным представлением данных с плавающей запятой, в том числе 4 – для преобразования между форматами HFP и BFP.
Для работы с HFP-данными появилось 26 новых команд, являющихся аналогами соответствующих BFP-команд. Эти новые команды включают, в частности, преобразования между форматами чисел с фиксированной и с плавающей запятой и новые операции с расширенной точностью.
В суперкомпьютерах NEC SX-4 (представленных в 1995 году) целые числа могут быть как 32-, так и 64-разрядными. Для чисел с плавающей запятой применяется стандарт IEEE 754 (как для 32-, так и для 64-разрядных чисел). Кроме того, SX-4 может работать со 128-разрядными числами с плавающей запятой расширенной точности и с форматами чисел с плавающей запятой, используемыми в PVP-системах Cray и мэйнфреймах IBM. При этом производительность SX-4 не зависит от формата представления, а сам этот формат выбирается при компиляции.