Пример выполнения контрольного задания (форма

Задание 1. Выполнить арифметические действия, рассматривая операнды как ЧФЗ справа от МЗР в формате 1-го байта. Определить модуль результата. Формат результата – 2 байта.

1. Выполним операцию сложения Z = X+Y = 18(10)

+ 33(10) = 51(10).

X = 18(10) = 0001 0010(2);       Y = 33(10) = 0010 0001(2).

Выполним сложение в ПК:

            Результат:    Z = 0011 0011(2) = 51(10)

.

2. Выполним операцию вычитания Z = X-Y = 18(10) – 33(10) = -15(10).

            Результат:    Z = 1000 1111(2) = 15(10) .

3. Выполним операцию умножения Z = X*Y = 18(10)*33(10)

= 594(10).

X = 18(10) = 0001 0010(2);       Y = 33(10) = 0010 0001(2).

Выполним операцию умножения младшими разрядами вперед:

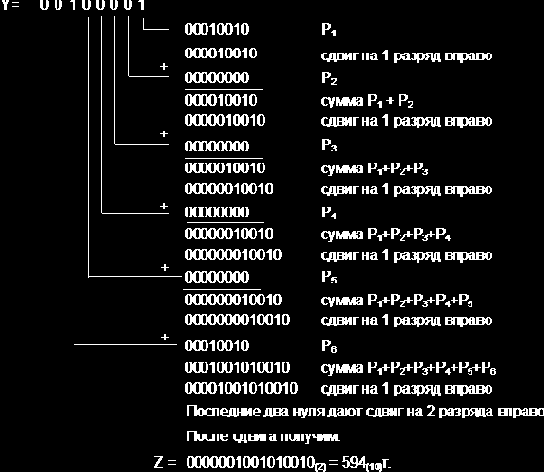
Задание 2. Выполнить арифметические действия, рассматривая операнды как ЧПЗ с основанием 2 в следующем формате: несмещенный порядок – 4 бита, мантисса – 8 бит. Формат результата – тот же. Округление производить после приведения операнда к нормализованной форме. Результат нормализовать.

X = 18.33(10);    Y = 33.18(10).

• Преобразуем дробную часть Х, равную 0.33(10), в двоичное число:


Таким образом, 0.33(10)

= 0.01010100(2), a X = 18.33(10) = 00010010.01010100(2).

• Представим X в формате ЧПЗ, округлив значение мантиссы до 8 разрядов (ненормализованное число):

• Нормализуем X:

• Преобразуем дробную часть Y, равную 0.18(10), в двоичное число:


Таким образом, 0.18(10) = 0.00101110(2), a Y = 33.18(10) = 00100001.00101110(2).

• Представим Y в формате ЧПЗ, округлив значение мантиссы до 8 разрядов (ненормализованное число):

• Нормализуем Y:


1. Выполним операцию сложения Z = X+Y = 18.33(10) + 33.18(10) = 51.51(10).





2. Выполним операцию вычитания Z = X-Y = 18.33(10)
+ 33.18(10) = -14.85(10).









Результат:    Z = (-) 0110 * 0.00111100(2) = - 26 * 0.234375 = - 15(10)
3). Выполним операцию умножения Z = X*Y = 18.33(10)*33.18(10) = 608.1894(10).





• Перемножим мантиссы сомножителей (вариант умножения младшими разрядами вперед):





















• Сложим порядки сомножителей:






• Нормализуем произведение:




Результат:       Z = 1010 * 0.10011000(2) = 210 * 0.59375(10)
= 608(10).
Задание 3.
Выполнить арифметические действия над операндами, представив их в двоично-десятичном коде.
1. Выполним операцию сложения Z=X+Y= 183(10) + 331(10)
= 514(10).
X = 183(10) = 0001 1000 0011(2-10); Y = 331(10) = 0011 0011 0001(2-10).





Результат:       Z = 0101 0001 0100(2-10)
= 514(10).
2. Выполним операцию вычитания Z = X – Y = 183(10) – 331(10)
= -148(10).

• Представим |Y| в ДК с избытком 6:





• Выполним сложение:




Отсутствие переноса из старшей тетрады является признаком того, что результат получился в ДК (т.е. отрицательный).

• Перейдем к нескорректированному избыточному ПК:





• Произведем коррекцию результата в соответствии с п. 5 алгоритма выполнения операции вычитания двоично-десятичных чисел:




Поскольку ранее результат получался в ДК, т.е. отрицательный, необходимо добавить знак (-).
Результат:       Z = - ( 0001 0100 1000)(2-10) = -148(10).
3. Выполним операцию умножения Z = X * Y = 183(10) * 331(10)
= 60573(10)
X = 183(10) = 0001 1000 0011(2-10); Y = 331(10) = 0011 0011 0001(2-10).
Для решения примера выберем вариант перемножения "младшие разряды вперед". В соответствии с п. 1 алгоритма полагаем сумму частичных произведений P0=0. (Частичные произведения будем обозначать Pi).



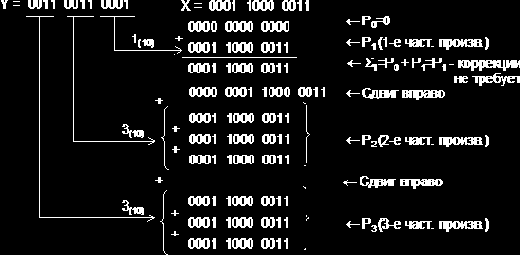
Формирование второго и третьего частичных произведений – более длительная операция, поскольку вторая и третья анализируемые тетрады содержат 3(10), поэтому каждая операция суммирования требует проверки необходимости коррекции.Вычислим P2 ( P2 = Р3 ), последовательно суммируя слагаемые, образующие P2:



Таким образом, второе (а также и третье) частичное произведение, состоящее из трех слагаемых, имеет вид   
P2 = Р3 = 0101 0100 1001(2-10).
Теперь можно вычислить сумму первого, второго и третьего частичного произведений, т.е. результат.



Окончательный результат: Z = 0110 0000 0101 0111 0011(2-10)
= 60573(10).

Содержание раздела



---







---