Геометрическая интерпретация линейного разделения классов

Пусть в нейроне в качестве функции активации используется ступенчатая функция (см. формулу (1) Лекции 2). Линейное разделяющее правило делит входное пространство на две части гиперплоскостью, классифицируя входные векторы как относящиеся к 1-му классу (выходной сигнал - 1) или 2-му классу (выходной сигнал - 0). Критическое условие классификации (уравнение разделяющей гиперплоскости)

$Геометрическая интерпретация линейного разделения классов$

В {

$Геометрическая интерпретация линейного разделения классов$

}-мерном пространстве (пространстве входных сигналов) разделяющая гиперплоскость перпендикулярна вектору

$Геометрическая интерпретация линейного разделения классов$

. Вектор входных сигналов

$Геометрическая интерпретация линейного разделения классов$

дает выход

$Геометрическая интерпретация линейного разделения классов$

, если его проекция

$Геометрическая интерпретация линейного разделения классов$

на вектор

$Геометрическая интерпретация линейного разделения классов$

больше, чем расстояние

$Геометрическая интерпретация линейного разделения классов$

от нуля до гиперплоскости. В

$Геометрическая интерпретация линейного разделения классов$

-мерном (расширенном) пространстве гиперплоскость, описываемая уравнением

$Геометрическая интерпретация линейного разделения классов$

, ортогональна вектору

$Геометрическая интерпретация линейного разделения классов$

и проходит через начало координат пространства признаков (образов).

Пример

В двухмерном пространстве входных сигналов уравнение гиперплоскости имеет вид

$Геометрическая интерпретация линейного разделения классов$

При

$Геометрическая интерпретация линейного разделения классов$

получаем уравнение

$Геометрическая интерпретация линейного разделения классов$

гиперплоскости, которая представлена на рис.1 пунктирной линией, пересекающей оси координат в точках (1.5, 0) и (0, 1.5) соответственно. Здесь:

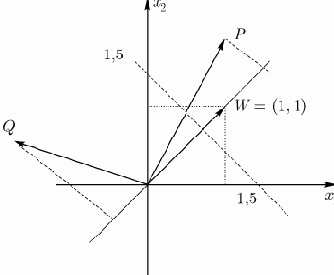
$Геометрическая интерпретация линейного разделения классов$

— нормаль к разделяющей гиперплоскости;

$Геометрическая интерпретация линейного разделения классов$

— вектор, относящийся к первому классу, поскольку проекция

$Геометрическая интерпретация линейного разделения классов$

вектора

$Геометрическая интерпретация линейного разделения классов$

на нормаль

$Геометрическая интерпретация линейного разделения классов$

больше

$Геометрическая интерпретация линейного разделения классов$

;

$Геометрическая интерпретация линейного разделения классов$

— вектор, относящийся ко второму классу, поскольку

$Геометрическая интерпретация линейного разделения классов$

Рис. 1.

Содержание раздела

Главная сайта