Автоассоциативная сеть Хопфилда

Структура сети Хопфилда представляется в виде системы с непосредственной обратной связью выхода со входом (рис. 1). Выходные сигналы нейронов являются одновременно входными сигналами сети:

. В классической сети Хопфилда отсутствует автосвязь (связь выхода нейрона с его собственным входом), что соответствует , а матрица весов является симметричной: . Отсутствие автосвязи и симметричность матрицы весов являются достаточными (но не необходимыми!) условиями сходимости итерационных (переходных) процессов в сети Хопфилда.

Далее в данной лекции предполагаем, что каждый нейрон имеет биполярную ступенчатую функцию активации со значениями

. Это означает, что выходной сигнал -го нейрона определяется функцией

где

обозначает количество нейронов, .

Далее допустим, что порог срабатывания является компонентой вектора

. Тогда основную зависимость, определяющую сеть Хопфилда, можно представить в виде

(1)

с начальным условием

.

В процессе функционирования сети Хопфилда можно выделить два режима: обучения и классификации. В режиме обучения на основе известных векторов подбираются весовые коэффициенты сети. В режиме классификации при фиксированных значениях весов и вводе конкретного начального состояния нейронов возникает переходный процесс вида (1), завершающийся в одном из локальных минимумов, для которого

.

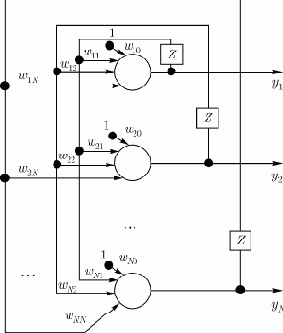
Рис. 1.  Структура сети Хопфилда

Содержание раздела

---

---

---

Главная сайта

---