Системы нечеткого вывода Мамдани-Заде
Элементы теории нечетких множеств, правила импликации и нечетких рассуждений образуют систему нечеткого вывода. В ней можно выделить:
- множество используемых нечетких правил;
- базу данных, содержащую описания функций принадлежности;
- механизм вывода и агрегирования, который формируется применяемыми правилами импликации.
В случае технической реализации в качестве входных и выходных сигналов выступают измеряемые величины, однозначно сопоставляющие входным значениям соответствующие выходные значения.
Для обеспечения взаимодействия этих двух видов вводится нечеткая система с так называемым фазификатором (преобразователем множеств входных данных в нечеткое множество) на входе и дефазификатором (преобразователем нечетких множеств в конкретное значение выходной переменной) на выходе.
Фазификатор преобразует точное множество входных данных в не\-четкое множество, определенное с помощью функции принадлежности, а~дефазификатор решает обратную задачу - формирует однозначное решение относительно входной переменной на основании многих нечетких выводов, вырабатываемых исполнительным модулем нечеткой системы.
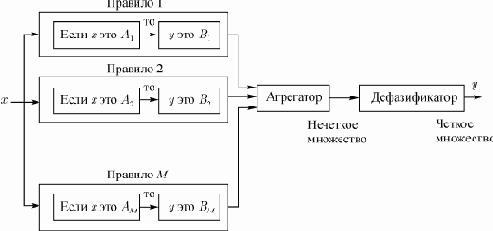
Рис. 1. Вывод в нечеткой системе при наличии M правил
Выходной сигнал модуля вывода может иметь вид

В модели вывода Мамдани-Заде присутствуют следующие операторы:
- оператор логического или арифметического произведения для определения результирующего уровня активации, в котором учитываются все компоненты вектора условия;
- оператор логического или арифметического произведения для определения значения функции принадлежности для всей импликации ;

- оператор логической суммы как агрегатор равнозначных результатов импликации многих правил;
- оператор дефазификации, трансформирующий нечеткий результат в четкое значение
 .
.
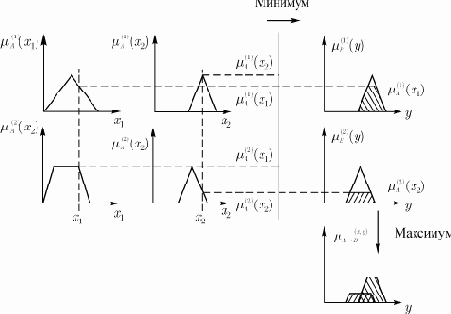
Рис. 2. Пример системы вывода Мамдани-Заде
На рис. 2 представлен способ агрегирования при двух входных переменных

Логическое произведение (оператор







